Introduction to Artificial Intelligence - Homework Assignment 05 (20pts.)¶
- NETIDs:
This assignment covers the following topics:
- Basic NLP Techniques
- Recurrent Neural Networks
- Transformers
It will consist of 6 tasks:
| Task ID | Description | Points |
|---|---|---|
| 00 | Cipher Classification and Dataset Creation | |
| 00-1 | - Bag-of-Words | 1 |
| 00-2 | - Bag-of-Characters | 1 |
| 00-3 | - Cipher Classification | 1 |
| 00-4 | - Dataset Creation | 0 |
| 01 | Recurrent Neural Network | |
| 01-1 | - Linear Layer | 0 |
| 01-2 | - Embedding Layer | 1 |
| 01-3 | - tanh Activation | 1 |
| 01-4 | - Recurrent Block | 1 |
| 01-5 | - Recurrent Neural Network | 1 |
| 01-6 | - RNN Training and Output | 1 |
| 02 | Torch Recurrent Neural Network Comparison | |
| 02-1 | - Torch RNN Class, Training, and Comparison | 1 |
| 02-2 | - RNN Short Answer Questions | 2 |
| 03 | Encoder-Only Transformer | |
| 03-1 | - ReLU Activation | 1 |
| 03-2 | - Self-Attention Block | 1 |
| 03-3 | - Encoder-Only Transformer | 1 |
| 03-4 | - Encoder-Only Transformer Training and Output | 1 |
| 04 | Torch Encoder-Only Transformer Comparison | |
| 04-1 | - Torch Positional Embeddings Class | 0 |
| 04-2 | - Torch Transformer Class | 1 |
| 04-3 | - Torch Transformer Training and Comparison | 1 |
| 04-4 | - Transformer Short Answer Questions | 2 |
| 05 | Final Evidence Collection | |
| 05-1 | - Selfie with Evidence | 1 |
Please complete all sections. Some questions may require written answers, while others may involve coding. Be sure to run your code cells to verify your solutions.
Story Progression¶
Thanks to your work on homework03 and homework04, the police were able to fully extract the text from the kidnapping letters:
"v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs phfuvat bgurejvfr v nz va erny gebhoyr"
Unfortunately, it appears that the text has been encoded somehow! As you try to recover from Thanksgiving break you realize that maybe you could treat this as a machine translation task. You could pretend the cipher is the source language and the plaintext is the target language.
If you could figure out the cipher then you could generate a training set of (cipher, plaintext) pairs. You could then train a seq2seq model to translate the ciphertext into plaintext!
Unfortunately because your professor hates you, he's making you write an RNN using only tensors for the first part of this assignment, and a transformer using on tensors on the second part. Use the dataset available from the github for training, testing, and validation on this assignment.
import torch
device = torch.device('cuda' if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu")
letter_text = "v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs phfuvat bgurejvfr v nz va erny gebhoyr"
Task 00: Text Similarity¶
Task 00-1: Description (0 pts.)¶
Bag-of-Words¶
Your first step is to figure out which cipher was most likely used to encode the kidnapping letters. To do this, you should test a Bag of Words and a Bag of Characters similarity metric. As with most of machine learning, we need to somehow convert our text into a vector to allow us to compare it to other vectors. One option would be to use a pre-trained embedding network like word2vec or GloVe (this would be like using the output of convolutional layers as features for MNIST). However, for now we will just use a Bag of Words and an N-Gram model instead (much simpler).
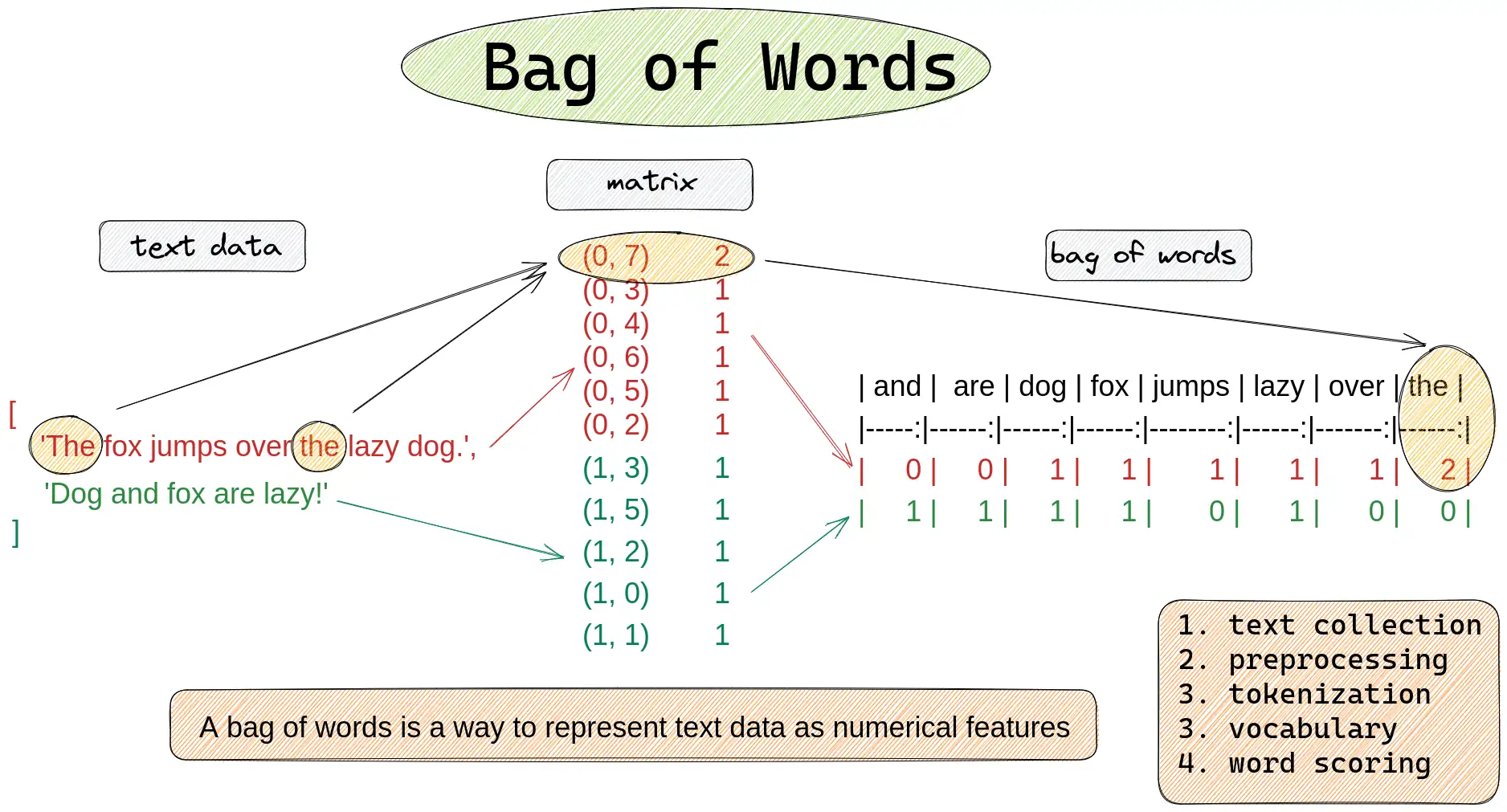
In the cell below, write the code for the Bag-of-Words comparison
Task 00-1: Code (1 pt.)¶
import math
from collections import Counter
def bow_similarity(text1, text2):
"""
Computes the cosine similarity between two texts based on word frequencies.
Splits the text on whitespace after converting to lower case.
"""
words1 = text1.lower().split()
words2 = text2.lower().split()
counter1 = Counter(words1)
counter2 = Counter(words2)
def dot(counter_a, counter_b):
return sum(counter_a[word] * counter_b[word] for word in counter_a)
# TODO: Compute the BoW similarity between two texts
if norm1 == 0 or norm2 == 0:
return 0.0
return dot_product / (norm1 * norm2)
Task 00-2: Description (0 pts.)¶
N-Gram/Bag-of-Characters Comparison¶
If you can remember all the way back to lecture07: Markov Models, you'll remember that we've actually seen these before, in the context of a Markov Babbler!
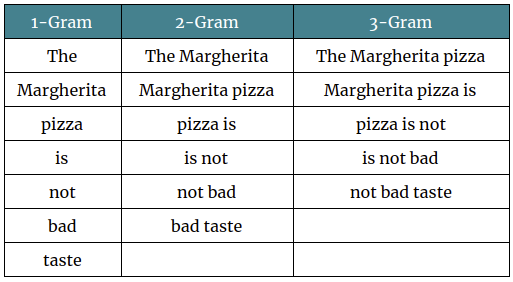
However for this task, I'd recommend using a character level N-Gram model instead, as we just want to compare character frequencies, it's tough to predict how ciphers will modify words and there's unlikely to be any overlap between the two.
Task 00-2: Code (1 pt.)¶
def boc_similarity(text1, text2):
"""
Computes the cosine similarity between two texts based on character frequencies.
Only considers alphanumeric characters after converting to lower case.
"""
counter1 = Counter(filter(str.isalnum, text1.lower()))
counter2 = Counter(filter(str.isalnum, text2.lower()))
def dot(counter_a, counter_b):
return sum(counter_a[ch] * counter_b[ch] for ch in counter_a)
# TODO: Compute the BoC similarity between two texts
if norm1 == 0 or norm2 == 0:
return 0.0
return dot_product / (norm1 * norm2)
Task 00-3: Description¶
Cipher Classification¶
To try and determine which cipher was used to encode our letter, we can encode a test string with various ciphers and see which of the encoded strings has the highest BoW and BoC with the kidnapping letter, essentially transforming this into a classification task! The ciphers to test are: Caesar, Vigenère, Substitution, Affine, and ROT13.
Task 00-3: Code (1 pt.)¶
from pycipher import Caesar, Affine, Vigenere, SimpleSubstitution
# Sample Lorem Ipsum text
text = ("Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.")
print("Original text:")
print(text)
# Encode using different ciphers
caesar_encoded = Caesar(3).encipher(text)
vigenere_encoded = Vigenere("key").encipher(text)
affine_encoded = Affine(5, 8).encipher(text)
substitution_encoded = SimpleSubstitution(key="phqgiumeaylnofdxjkrcvstzwb").encipher(text)
rot13_encoded = Caesar(13).encipher(text)
# Show the encoded texts
print("\nEncoded texts:")
print("Caesar Cipher: ", caesar_encoded)
print("Vigenère Cipher: ", vigenere_encoded)
print("Substitution Cipher:", substitution_encoded)
print("Affine Cipher: ", affine_encoded)
print("ROT13: ", rot13_encoded)
letter_string = "v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs phfuvat bgurejvfr v nz va erny gebhoyr"
print('Kidnapping letter text:', letter_string)
# Save the encoded texts in a dictionary for easy iteration
encoded_versions = {
"Caesar": caesar_encoded,
"Vigenère": vigenere_encoded,
"Substitution": substitution_encoded,
"Affine": affine_encoded,
"ROT13": rot13_encoded
}
# TODO: Calculate and print the BoW similarities between the encoded sample texts and the letter text
print("\nBag-of-Words (BoW) similarity with test string:")
# TODO: Calculate and print the BoC similarities between the encoded sample texts and the letter text
print("\nBag-of-Characters (BoC) similarity with test string:")
Expected Output¶
Original text:
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
Encoded texts:
Caesar Cipher: Oruhp lsvxp groru vlw dphw, frqvhfwhwxu dglslvflqj holw, vhg gr hlxvprg whpsru lqflglgxqw xw oderuh hw groruh pdjqd doltxd.
Vigenère Cipher: Vspoq gzwsw hmvsp cmr kqcd, gmxwcmxcdyp khgzmqmmlq ijsx, qoh by igewkyh roqnyv gxggnmberr ex jkfmbi cd hmvspo qyqry kpgayy.
Substitution Cipher: Sgktd ohlxd rgsgk loz qdtz, egflteztzxk qroholeofu tsoz, ltr rg toxldgr ztdhgk ofeororxfz xz sqwgkt tz rgsgkt dqufq qsojxq.
Affine Cipher: Lapcq wfueq xalap uwz iqcz, savucszczep ixwfwuswvm clwz, ucx xa cweuqax zcqfap wvswxwxevz ez linapc cz xalapc qimvi ilwkei.
ROT13: Yberz vcfhz qbybe fvg nzrg, pbafrpgrghe nqvcvfpvat ryvg, frq qb rvhfzbq grzcbe vapvqvqhag hg ynober rg qbyber zntan nyvdhn.
Kidnapping letter text: v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs phfuvat bgurejvfr v nz va erny gebhoyr
Bag-of-Words (BoW) similarity with test string:
Caesar : 0.0000
Vigenère : 0.0000
Substitution: 0.0000
Affine : 0.0000
ROT13 : 0.0000
Bag-of-Characters (BoC) similarity with test string:
Caesar : 0.6023
Vigenère : 0.6518
Substitution: 0.5527
Affine : 0.4254
ROT13 : 0.9198
Story Progression¶
It definitely looks like the text was a ROT13 cipher! Now we could of course just directly use the ROT13 cipher to decode the text, but where's the fun in that? AI is the future right! You're using it to replace your ability to do even the most basic thinking tasks so obviously we should also use it here instead of just the closed form solution!
What we need to do now is create a dataset of (ciphertext, plaintext) pairs to train a seq2seq model to decode the ciphertext. Luckily, we can use a library called NLTK to get a list of words in the English language. We can use this list to generate a dataset of (ciphertext, plaintext) pairs.
Task 00-4: Description (0 pts.)¶
Dataset creation¶
NLTK: Natural Language Toolkit is one of the most popular libraries for working with text in Python. It's a great tool to have in your toolbelt.
In the cell below lets create our dataset of (ciphertext, plaintext) pairs. We can start with 10000 "sentences" and lets see how well the model does.
Task 00-4: Code (0 pts.)¶
import math
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, TensorDataset, DataLoader
from torch.nn.utils.rnn import pad_sequence
import nltk
import codecs
import numpy as np
import torch
import string
import torch.nn.functional as F
import random
from collections import namedtuple
class Rot13Dataset(Dataset):
def __init__(self, word_list, device="cpu", one_hot_targets=True):
# ---- vocab (owned by the dataset) ----
self.vocab = ('<PAD>','<EOS>','<UNK>','<SOS>',' ') + tuple(string.ascii_lowercase) # 31
self.vocab_size = len(self.vocab)
self.char2idx = {ch:i for i,ch in enumerate(self.vocab)}
self.idx2char = {i:ch for i,ch in enumerate(self.vocab)}
self.padding_idx = self.char2idx['<PAD>']
self.device = device
self.one_hot_targets = one_hot_targets
words = [w.lower() for w in word_list if w.isalpha()]
self.data = []
for _ in range(10000): # choose your dataset size
k = random.randint(3, 12)
phrase = " ".join(random.choices(words, k=k))
rot = codecs.encode(phrase, 'rot_13')
src = torch.tensor([self.char2idx.get(c, self.char2idx['<UNK>']) for c in rot], dtype=torch.long)
tgt = torch.tensor([self.char2idx.get(c, self.char2idx['<UNK>']) for c in phrase], dtype=torch.long)
self.data.append((src, tgt))
# ---------- helpers ----------
def encode(self, s): # string -> 1D LongTensor
return torch.tensor([self.char2idx.get(c, self.char2idx['<UNK>']) for c in s], dtype=torch.long)
def decode(self, idxs): # 1D LongTensor -> string
return ''.join(self.idx2char[int(i)] for i in idxs)
# ---------- Dataset API ----------
def __len__(self): return len(self.data)
def __getitem__(self, i): return self.data[i] # (T,), (T,)
# ---------- Collate (pad, optional one-hot, move to device) ----------
def collate(self, batch):
X_list, Y_list = zip(*batch) # tuples of 1D tensors
X = pad_sequence(X_list, batch_first=True, padding_value=self.padding_idx) # (B,T)
Y_idx = pad_sequence(Y_list, batch_first=True, padding_value=self.padding_idx) # (B,T)
Y = F.one_hot(Y_idx.clamp_min(0), num_classes=self.vocab_size).float() # (B,T,V)
return X.to(self.device), Y.to(self.device)
# Get words from NLTK and take a subset.
# Download the NLTK 'words' corpus if needed.
nltk.download('words')
from nltk.corpus import words
word_list = words.words()
filtered_words = [w for w in word_list if w.isalpha()]
dataset = Rot13Dataset(filtered_words, device=device)
train_loader = DataLoader(dataset, batch_size=64, shuffle=True, collate_fn=dataset.collate)
print(f"Total training samples: {len(dataset)}")
Story Progression¶
Given this dataset, we now need a seq2seq model to decode the ciphertext. We'll start with a simple RNN model that you'll need to implement in numpy
Task 01: Recurrent Neural Network¶

Remember that unlike a FFN, data in an RNN loops around over the sequence of inputs, to allow us to build up a hidden state (context in my words) that can be used to generate the next output. There's a really good cheatsheet from Stanford about RNNs that I'd recommend.
NOTE: We can re-use a few parts of our FFN from Homework04 and I'd recommend you lean on your solution heavily while writing this homework.
Task 01-1: Description (0 pts.)¶
Linear Layer¶
Firstly, we'll need a linear layer again which you may consider reusing from Homework04
Task 01-1: Code (0 pts.)¶
# TODO: Implement the LinearLayer class (Consider copying from Homework04)
Task 01-2: Description (0 pts.)¶
Embedding Layer¶
Now that we have an output layer, we only need three more components for our RNN. One of those is the embedding layer, which will take our tokenized input and transform it into an embedding. Luckily this is extremely similar to a linear layer. Therefore we can inherit most of the code from that and just rewrite the forward function a little bit.
Task 01-2: Code (1 pt.)¶
class EmbeddingLayer(LinearLayer):
"""
An embedding layer
Attributes:
W (numpy.ndarray): Weight matrix with shape (output_dim, input_dim).
b (numpy.ndarray): Bias vector with shape (output_dim, 1).
vocab_size (int): Size of the vocabulary
X (numpy.ndarray): Cached input used during the forward pass.
dW (numpy.ndarray): Gradient with respect to the weights.
db (numpy.ndarray): Gradient with respect to the biases.
"""
def __init__(self, vocab_size, embed_dim, device="cpu"):
"""
Initialize the EmbeddingLayer using the constructor from the LinearLayer
Args:
vocab_size (int): Number of tokens in the vocab
embed_dim (int): Size of the token embedding
"""
# call the LinearLayer constructor
super().__init__(input_dim=vocab_size, output_dim=embed_dim, device=device)
self.vocab_size = vocab_size
def forward(self, X_idx):
"""
Compute the forward pass of the embedding layer.
Args:
X_idx (torch.Tensor): Input data with shape (batch_size, sequence_length, vocab_size)
Returns:
torch.Tensor: Linear output with shape (batch_size, sequence_length, embedding_dim)
Notes:
The bias is disabled as it is not used in the embedding layer.
"""
# TODO: Implement the forward pass for the embedding layer
# Build one-hot so LinearLayer can do its usual math
class Tanh:
"""
The tanh activation function
Attributes:
None
"""
def forward(self, X):
"""
Compute the forward pass of the tanh activation function
Args:
X (torch.Tensor): Input data with shape (batch_size, sequence_length, )
Returns:
torch.Tensor: the tanh of the input X
"""
# TODO: Return the tanh activation
def backward(self, dA):
"""
Compute the backward pass of the tanh activation function
Args:
dA (torch.Tensor): Gradient data with shape (batch_size, sequence_length, hidden_size)
Returns:
torch.Tensor: dA passed into the derivative of tanh
"""
# TODO: Return the derivative of tanh
def update(self, lr):
"""
Update the parameters of the layer using gradient descent.
Args:
lr (float): Learning rate for the parameter update.
Returns:
None
"""
# TODO: Update the parameters with learning rate lr
class RecurrentBlock:
"""
A Recurrent Block
Attributes:
W (torch.Tensor): Input Weight matrix with shape (hidden_size, input_dim).
U (torch.Tensor): Hidden Weight matrix with shape (hidden_size, hidden_size).
b (torch.Tensor): Bias vector with shape (hidden_size).
Grad_Info (namedtuple): Cached hidden state info using the Grad_Info tuple made in forward and used in backward
dW (torch.Tensor): Gradient with respect to the input weights.
dU (torch.Tensor): Gradient with respect to the hidden weights.
db (torch.Tensor): Gradient with respect to the biases.
"""
Grad_Info = namedtuple('Grad_Info', ['x_at_timestep', 'h_at_timestep', 'h_prev_at_timestep'])
def __init__(self, input_dim, hidden_size, device='cpu'):
self.input_dim = input_dim # This should match the embedding size.
self.hidden_size = hidden_size
self.device = device
self.W = torch.randn(hidden_size, input_dim, device=self.device) * math.sqrt(2.0 / input_dim)
self.U = torch.randn(hidden_size, hidden_size, device=self.device) * math.sqrt(2.0 / input_dim)
self.b = torch.zeros(hidden_size, device=self.device)
self.activation = Tanh()
self.hidden_states = []
def forward(self, X):
"""
Compute the forward pass of the recurrent block over the entire input sequence
Args:
X (torch.Tensor): embedded input with shape: (batch_size, sequence_len, hidden_size)
Returns:
self.outputs (torch.Tensor): matrix containing the hiddent state at each timestep with shape: (batch_size, sequence_len, hidden_size)
"""
batch_size, seq_len, _ = X.shape
outputs = []
self.hidden_states = [self.Grad_Info(
x_at_timestep=None,
h_at_timestep=torch.zeros((batch_size, self.hidden_size), device=self.device),
h_prev_at_timestep=None
)]
for timestep in range(seq_len):
x_at_timestep = X[:, timestep, :]
# TODO: Compute the forward pass for each item in the sequence
outputs.append(h_at_timestep)
# Stack outputs along the time-axis: (batch_size, seq_len, hidden_size)
self.outputs = torch.stack(outputs, dim=1)
return self.outputs
def backward(self, d_outputs):
"""
Compute the backward pass of the recurrent block using backpropagation through time (BPTT)
Args:
d_outputs (torch.Tensor): Gradient with respect to outputs with shape: (batch_size, sequence_len, hidden_size)
Returns:
torch.Tensor: dX after BPTT is performed with shape: (batch_size, sequence_len, embedding_size)
"""
# d_outputs:
batch_size, seq_len, hidden_size = d_outputs.shape
dW = torch.zeros_like(self.W, device=self.device)
dU = torch.zeros_like(self.U, device=self.device)
db = torch.zeros_like(self.b, device=self.device)
dX = torch.zeros((batch_size, seq_len, self.input_dim), device=self.device)
dh_next = torch.zeros((batch_size, hidden_size), device=self.device) # Gradient propagated from future time steps.
for backwards_timestep in list(reversed(range(seq_len))):
# TODO: Compute the backward pass for each item in the sequence
self.dW = dW
self.dU = dU
self.db = db
return dX
def update(self, lr):
"""
Update the parameters of the block using gradient descent.
Args:
lr (float): Learning rate for the parameter update.
Returns:
None
"""
# TODO: Update the parameters with learning rate lr
Task 01-5: Description (0 pts.)¶
Recurrent Neural Network¶
Now that we have the components of an RNN (embedding_layer -> recurrent_block -> output_layer) and the tanh activation function, we can combine them all in a RecurrentNeuralNetwork class similarly to the FeedForwardNetwork in Homework04 (you again may consider pulling heavily from that for identical components)!
Task 01-5: Code (1 pt.)¶
from typing import Any
class RecurrentNeuralNetwork:
def __init__(self, vocab_size, embed_size, hidden_size, padding_idx=0, device='cpu'):
self.vocab_size = vocab_size
self.embed_size = embed_size
self.hidden_size = hidden_size
self.padding_idx = padding_idx
self.device = device
# TODO: Initialize the 3 components of the RNN
# Layers:
embedding_layer = EmbeddingLayer(vocab_size, embed_size, device=device)
# For the recurrent context layer, the input dimension is the embed_size.
recurrent_block = RecurrentBlock(embed_size, hidden_size, device=device)
# Final fully connected layer: project hidden state to vocabulary logits.
output_layer = LinearLayer(hidden_size, vocab_size, device=device)
# Keep model layers in a list for easy backward and update passes.
self.layers = [embedding_layer, recurrent_block, output_layer]
def forward(self, X, eval=False):
"""
Args:
x: (batch_size, seq_len) with integer token indices.
Returns:
logits: (batch_size, seq_len, vocab_size)
outputs: (batch_size, seq_len, hidden_size) final hidden states over time.
"""
# TODO: Calculate the output of the network
return X if not eval else self.softmax(X)
def backward(self, Y_hat, Y):
# TODO: Calculate the gradient of the loss with respect to the input
def softmax(self, X):
"""
Args:
X (torch.Tensor): Input data with shape (n_classes, m), where n_classes is the number of classes
and m is the number of examples.
Returns:
torch.Tensor: Softmax probabilities with shape (n_classes, m).
"""
# TODO: Store the input and calculate the output of the softmax layer
def cross_entropy(self, logits, Y):
"""
Compute the cross-entropy loss.
Args:
Y_hat (numpy.ndarray): Predicted probability matrix of shape (n_classes, m).
Y (numpy.ndarray): One-hot encoded true labels of shape (n_classes, m).
Returns:
float: The average cross-entropy loss over all m examples.
Notes:
A small constant epsilon is added to Y_hat to avoid computing log(0).
"""
# TODO: Calculate the cross-entropy loss
def get_accuracy(self, logits, Y):
"""
Compute the classification accuracy.
Args:
Y_hat (numpy.ndarray): Predicted probability matrix from the network, shape (n_classes, m).
Y (numpy.ndarray): One-hot encoded true labels, shape (n_classes, m).
Returns:
float: Accuracy as a fraction between 0 and 1.
"""
# TODO: Calculate the accuracy of the network
def test_on_letter(self, dataset):
kidnapping_letter = "v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr" # ROT13 of "hello"
x = dataset.encode(kidnapping_letter).unsqueeze(0).to(self.device) # (1, T)
preds = self.forward(x, eval=True)
preds = preds.argmax(dim=-1) # (1, T)
# x = dataset.decode(preds).unsqueeze(0).to(self.device) # (1, T)
predicted_deciphered = "".join(dataset.idx2char[int(i)] for i in preds.squeeze(0))
print(f"\tInput (ROT13): {kidnapping_letter}")
print(f"\tPredicted original: {predicted_deciphered}")
return predicted_deciphered
def train(self, train_loader, epochs=100, learning_rate=0.001, verbose=True):
"""
Train the neural network using mini-batch gradient descent.
Args:
X (numpy.ndarray): Input data with shape (784, m), where each column is a flattened MNIST style image.
Y (numpy.ndarray): One-hot encoded labels with shape (n_classes, m), where n_classes is 26
epochs (int): Number of epochs for training.
learning_rate (float): Learning rate for the parameter updates.
batch_size (int, optional): Number of examples per mini-batch. Default is 32.
verbose (bool, optional): If True, prints training progress every 500 epochs. Default is False.
Returns:
dict: A dictionary containing:
- 'loss_history': List of loss values for each epoch.
- 'accuracy_history': List of accuracy values for each epoch.
Process:
- Shuffles the dataset each epoch.
- Processes data in mini-batches.
- Performs a forward pass, backpropagation, and parameter updates for each mini-batch.
- Computes the loss and accuracy for the entire dataset after each epoch.
"""
loss_history = []
accuracy_history = []
for i in range(epochs):
batch_losses = []
batch_accuracies = []
for X_batch, Y_batch in train_loader:
# Forward propagation
# TODO: Calculate the output of the network
# Calculate metrics for the whole epoch
loss = self.cross_entropy(Y_hat_batch, Y_batch)
accuracy = self.get_accuracy(Y_hat_batch, Y_batch)
batch_losses.append(loss.item())
batch_accuracies.append(accuracy.item())
# Backward propagation
# TODO: Calculate the gradients of the loss with respect to the input
# Update parameters
# TODO: Update the weights and biases of the layer using the learning rate
loss_history.append(np.mean(batch_losses))
accuracy_history.append(np.mean(batch_accuracies))
if verbose and i % (epochs // 4) == 0:
print(f"Epoch {i+1}/{epochs}")
print(f"loss: {loss_history[-1]:.5f}")
print(f"accuracy: {accuracy_history[-1]:.5f}")
print('Output test:')
self.test_on_letter(train_loader.dataset)
print("-" * 30)
return {'loss_history': loss_history, 'accuracy_history': accuracy_history}
# TODO: Instantiate and train our RNN
Task 01-6: Reference Output (0 pts.)¶
Approximate Runtime: 7m 31.9s
Epoch 1/100
loss: 9.22425
accuracy: 0.01539
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: asua astxjaejabvmyjs<UNK>r<EOS>avbesbamasl<UNK>s<UNK>r<EOS>lbv<UNK>l<UNK>qs<UNK>r<EOS>ljlrsmlrs<UNK>r<EOS>lksjrxo<UNK>srdjaejsrhlljmmyesvajchyahljc<UNK>slal<SOS>mma<UNK>rla<UNK>slrsm<EOS>hhlrjny<UNK>achmfyjfjammjyyajcvsja<UNK>s<UNK>r<EOS>loa qabl<UNK>ajmmj s<UNK>r<EOS>lklabaomsl<EOS>oaesjmmbaomcjsjmm<UNK>r<EOS>lvboauas ujjjsj skf<UNK>xsj<UNK>r<EOS>jdavbsysl<EOS>labmjcacl<UNK>jaanrd
------------------------------
Epoch 26/100
loss: 1.78745
accuracy: 0.80328
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i lo fd sprdering yr thwisoedloyd at thw estate thw <EOS>as das thw psrroct sdrder lhapon ie smre ill <EOS>et aaa<SOS> mith it as dpdl hopywully yofodm iigres out thw corcination og thw padlocu adcde on locucr on thw soaond seoor og itx othwrdiso i ag in real troufle
------------------------------
Epoch 51/100
loss: 1.20777
accuracy: 0.86253
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i lo ld furdering yr theiseedloyd at the estate the <EOS>as <EOS>as the perrgct purder loapon ie sure ill <EOS>et aaay mith it as <EOS>ell hopewully yobody iibres out the coueination og the padlocu adcde on locucr on the seaond seoor og itx othwrkise i ap in real trouele
------------------------------
Epoch 76/100
loss: 0.97005
accuracy: 0.89484
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i lofld furdering er theisenfloyd at the estate the eas <EOS>as the pdregct burder loapon ie sure ill eet aaay mith it as <EOS>ell hopepully nobody iiures out the coueination of the padlocu adcde on locucr on the second sloor of itx oth<UNK>rkise i ap in real trouble
------------------------------
Story Progression¶
I'm not going to show you the exact out of the kidnapping letter as that'd spoil some of the surprise but absolutely do NOT expect to get perfectly clean english out of this, I could make out most of the words but it's pretty garbled and unfortunately because it's not perfect we can't quite get the correct padlock combination from it. Lets see if the built-in RNN from torch does any better!
Task 02: RNN Comparisons¶
Task 02-1: Description (0 pts.)¶
RNN Class Instantiation¶
Lets use the torch builtins to make an RNN and compare it against our handmade one to see if it does any better!
Task 02-1: Code (1 pt.)¶
import torch
import torch.nn as nn
device = torch.device('cuda' if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu")
kidnapping_letter = "v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr" # ROT13 of "hello"
vocab_size = dataset.vocab_size
embed_size = 32
hidden_size = 64
class CharRNN(nn.Module):
def __init__(self, vocab_size, embed_size, hidden_size):
super().__init__()
# TODO: Instantiate the embedding, RNN, and linear layers
def forward(self, x, h0=None):
# TODO: Implement the forward pass
# TODO: Instantiate the model, optimizer, and loss function
rnn_model.train()
for epoch in range(100):
total_loss = 0.0
correct = 0
count = 0
for xb, yb in train_loader:
rnn_optimizer.zero_grad()
# TODO: Call the forward pass
B, T, V = logits.shape
# If yb is one-hot (B, T, V), convert to indices (B, T)
if yb.dim() == 3:
# Assumes last dim is vocab dimension
yb = yb.argmax(dim=-1) # (B, T)
# flatten for CrossEntropyLoss
logits_flat = logits.reshape(B * T, V) # (B*T, vocab)
yb_flat = yb.reshape(B * T) # (B*T,)
# TODO: Calculate the loss and backpropagate
total_loss += loss.item()
preds = logits_flat.argmax(dim=-1)
correct += (preds == yb_flat).sum().item()
count += yb_flat.size(0)
avg_loss = total_loss / len(train_loader)
accuracy = correct / count
if epoch % 25 == 0:
print(f"Epoch {epoch+1} | loss: {avg_loss:.5f} | accuracy: {accuracy:.5f}")
rnn_model.eval()
x = dataset.encode(kidnapping_letter).unsqueeze(0).to(device) # (1, T)
preds, _ = rnn_model.forward(x)
preds = preds.argmax(dim=-1) # (1, T)
predicted_deciphered = "".join(dataset.idx2char[int(i)] for i in preds.squeeze(0))
print(f"\tInput (ROT13): {kidnapping_letter}")
print(f"\tPredicted original: {predicted_deciphered}")
rnn_model.train()
Task 02-1: Reference Output (0 pts.)¶
Approximate Runtime: 7m 34.5s
Epoch 1 | loss: 0.92368 | accuracy: 0.86896
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenfloyd at the estate the gas oas the perfect murder oeapon im sure ill get aoay oith it as oell hopefully nobody figures out the combination of the padloce abcde on loceer on the second floor of fity otheroise i am in real trouble
Epoch 26 | loss: 0.00013 | accuracy: 1.00000
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenfloyd at the estate the gas was the perfect murder weapon im sure ill get away with it as well hopefully nobody figures out the combination of the padlock abcde on locker on the second floor of fitz otherwise i am in real trouble
Epoch 51 | loss: 0.00001 | accuracy: 1.00000
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenfloyd at the estate the gas was the perfect murder weapon im sure ill get away with it as well hopefully nobody figures out the combination of the padlock abcde on locker on the second floor of fitz otherwise i am in real trouble
Epoch 76 | loss: 0.00000 | accuracy: 1.00000
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenfloyd at the estate the gas was the perfect murder weapon im sure ill get away with it as well hopefully nobody figures out the combination of the padlock abcde on locker on the second floor of fitz otherwise i am in real trouble
Task 02-2: RNN Short Answer Questions (2 pts.)¶
Why do we need to do "Backprop through time" for RNNs?
- [ANSWER]
Why do we have two weight matrices in the recurrent block?
- [ANSWER]
Task 03: Encoder-Only Transformer¶
Task 03-1: Description (0 pts.)¶
Self-Attention Block¶
Transformers are really a direct improvement on RNNs as a sequence model. Our hand-made RNN struggled with the task, so lets see if a transformer can do any better! This is pretty tricky so we'll only write a little bit of it.
Task 03-1: Code (1 pt.)¶
import math
import torch
import torch.nn.functional as F
from collections import namedtuple
class SelfAttentionBlock:
Grad_Info = namedtuple('Grad_Info', [
'x', # (B, T, C) input
'q', 'k', 'v', # (B, T, Dh)
'scores', # (B, T, T)
'attn', # (B, T, T)
'attn_v', # (B, T, Dh) = attn @ v
'out_before_proj' # (B, T, Dh) = attn_v (alias for clarity)
])
def __init__(self, model_dim, head_dim=None, device='cpu'):
"""
Single-head self-attention for clarity.
model_dim: C (embedding size)
head_dim: Dh (defaults to model_dim)
"""
self.C = model_dim
self.Dh = head_dim if head_dim is not None else model_dim
assert self.Dh == self.C, "For this simple single-head block, set head_dim == model_dim."
self.device = device
# Parameters (weights are (out_dim, in_dim) to match @ x.T usage)
scale_in = math.sqrt(2.0 / self.C)
self.Wq = torch.randn(self.Dh, self.C, device=self.device) * scale_in
self.Wk = torch.randn(self.Dh, self.C, device=self.device) * scale_in
self.Wv = torch.randn(self.Dh, self.C, device=self.device) * scale_in
self.bq = torch.zeros(self.Dh, device=self.device)
self.bk = torch.zeros(self.Dh, device=self.device)
self.bv = torch.zeros(self.Dh, device=self.device)
self.Wo = torch.randn(self.C, self.Dh, device=self.device) * math.sqrt(2.0 / self.Dh)
self.bo = torch.zeros(self.C, device=self.device)
self.cache = None # holds Grad_Info from the last forward
def forward(self, X, key_pad_mask=None, causal=False):
"""
X: (B, T, C)
key_pad_mask: optional (B, T) bool; True where PAD token — disallow attending to those keys.
causal: if True, apply lower-triangular mask (not needed for ROT13, included for pedagogy).
Returns: Y = X + proj(Attn(X)) (B, T, C)
"""
B, T, C = X.shape
# TODO: Calculate Q, K, and V
# TODO: Calculate the scaled dot-product scores
# Masks (optional)
if key_pad_mask is not None:
# Disallow attending to PAD keys (set scores to -inf for those columns)
# key_pad_mask: True where PAD
mask_k = key_pad_mask.unsqueeze(1).expand(B, T, T) # broadcast over query length
scores = scores.masked_fill(mask_k, float('-inf'))
if causal:
tril = torch.tril(torch.ones(T, T, device=X.device, dtype=torch.bool))
scores = scores.masked_fill(~tril, float('-inf'))
# TODO: Calculate the softmax over keys
# TODO: Calculate the attention vectors
# TODO: Calculate the output projection, then add the residual
# Cache for backward
self.cache = SelfAttentionBlock.Grad_Info(
x=X, q=Q, k=K, v=V, scores=scores, attn=attn,
attn_v=attn_v, out_before_proj=out_before_proj
)
return Y
def backward(self, dY, key_pad_mask=None, causal=False):
"""
dY: gradient wrt output Y, shape (B, T, C)
Returns: dX (B, T, C)
Computes and accumulates parameter grads in self.dW*, self.db*.
"""
B, T, C = dY.shape
cache = self.cache
# Y = X + y_ctx
dy_ctx = dY.clone() # (B, T, C) branch gradient through context path
dX = dY.clone() # residual path contributes identity
# y_ctx = attn_v @ Wo^T + bo
# grads for Wo, bo, and attn_v
# dWo = sum_over_batch,time ( dy_ctx[b,t,:]^T @ attn_v[b,t,:] )
self.dWo = dy_ctx.reshape(-1, C).T @ cache.attn_v.reshape(-1, self.Dh)
self.dbo = dy_ctx.sum(dim=(0, 1))
dattn_v = dy_ctx @ self.Wo # (B, T, Dh)
# attn_v = attn @ v
dv = cache.attn.transpose(1, 2) @ dattn_v # (B, T, Dh)
dattn = dattn_v @ cache.v.transpose(1, 2) # (B, T, T)
# Softmax backward:
# Given A = softmax(S), dL/dS = (dL/dA - sum(dL/dA * A, axis=-1, keepdim=True)) * A
tmp = (dattn * cache.attn).sum(dim=-1, keepdim=True) # (B, T, 1)
dscores = (dattn - tmp) * cache.attn # (B, T, T)
# Respect masks in backward (optional, mirrors forward)
if key_pad_mask is not None:
mask_k = key_pad_mask.unsqueeze(1).expand(B, T, T) # True where PAD (disallowed)
dscores = dscores.masked_fill(mask_k, 0.0)
if causal:
tril = torch.tril(torch.ones(T, T, device=dY.device, dtype=torch.bool))
dscores = dscores.masked_fill(~tril, 0.0)
# scores = (q @ k^T) / sqrt(Dh)
factor = 1.0 / math.sqrt(self.Dh)
dqk = dscores * factor # (B, T, T)
# grads wrt q and k via matmul rules
dq = dqk @ cache.k # (B, T, Dh)
dk = dqk.transpose(1, 2) @ cache.q # (B, T, Dh)
# q = X Wq^T + bq ; k = X Wk^T + bk ; v = X Wv^T + bv
# Accumulate parameter grads
# dW = sum_over_batch,time ( dproj[b,t,:]^T @ X[b,t,:] )
self.dWq = dq.reshape(-1, self.Dh).T @ cache.x.reshape(-1, self.C)
self.dbq = dq.sum(dim=(0, 1))
self.dWk = dk.reshape(-1, self.Dh).T @ cache.x.reshape(-1, self.C)
self.dbk = dk.sum(dim=(0, 1))
self.dWv = dv.reshape(-1, self.Dh).T @ cache.x.reshape(-1, self.C)
self.dbv = dv.sum(dim=(0, 1))
# dX accumulates contributions from Q/K/V branches
dX += dq @ self.Wq
dX += dk @ self.Wk
dX += dv @ self.Wv
return dX
def update(self, lr):
# SGD update (swap for Adam if you want)
self.Wq -= lr * self.dWq; self.bq -= lr * self.dbq
self.Wk -= lr * self.dWk; self.bk -= lr * self.dbk
self.Wv -= lr * self.dWv; self.bv -= lr * self.dbv
self.Wo -= lr * self.dWo; self.bo -= lr * self.dbo
class ReLU:
"""
Element-wise rectified linear activation.
"""
def forward(self, X):
"""
Apply ReLU activation and cache the input tensor.
Args:
X (torch.Tensor): Input tensor of any shape.
Returns:
torch.Tensor: Tensor with negatives zeroed out, same shape as `X`.
"""
# TODO: Store the input and calculate and return the output of the ReLU layer
def backward(self, dA):
"""
Propagate gradients through the ReLU non-linearity.
Args:
dA (torch.Tensor): Upstream gradient matching the shape of the forward output.
Returns:
torch.Tensor: Gradient with respect to the input, zeroed where the cached input was non-positive.
"""
# TODO: Calculate and return the gradient of the loss with respect to the input
def update(self, lr):
"""
Keep API parity with trainable layers; ReLU has no parameters to update.
Args:
lr (float): Unused learning rate argument.
Returns:
None
"""
# TODO: Update the weights and biases of the layer using the learning rate
Task 03-3: Description (0 pts.)¶
Encoder-only Transformer Model¶
Similar to our FFN and RNN, lets make an EncoderTransformer class to house all of the components for our transformer model. We'll make a model with two attention blocks. GPT-3 is just one of these models but with 96 attention blocks (and trained on like the entirety of the internet)!
Task 03-3: Code (1 pt.)¶
device = torch.device('cuda' if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu")
class EncoderTransformer:
def __init__(self, vocab_size: int, padding_idx: int, ctx_len: int = 256, d_model: int = 128):
self.padding_idx = padding_idx
self.ctx_len = ctx_len
self.device = torch.device('cuda' if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu")
# TODO: Instantiate the components of the transformer
def forward(self, X, eval=False):
"""
Args:
x: (batch_size, seq_len) with integer token indices.
Returns:
logits: (batch_size, seq_len, vocab_size)
outputs: (batch_size, seq_len, hidden_size) final hidden states over time.
"""
# TODO: Calculate the output of the network
return X if not eval else self.softmax(X)
def backward(self, Y_hat, Y):
# TODO: Calculate the gradient of the loss with respect to the input
def softmax(self, X):
"""
Apply softmax to the input tensor.
Args:
X (torch.Tensor): Input tensor of any shape.
Returns:
torch.Tensor: Tensor with softmax applied, same shape as `X`.
"""
return F.softmax(X, dim=-1)
def cross_entropy(self, Y_hat, Y):
"""
Compute the cross-entropy loss.
Args:
Y_hat (numpy.ndarray): Predicted probability matrix of shape (n_classes, m).
Y (numpy.ndarray): One-hot encoded true labels of shape (n_classes, m).
Returns:
float: The average cross-entropy loss over all m examples.
Notes:
A small constant epsilon is added to Y_hat to avoid computing log(0).
"""
# TODO: Calculate the cross-entropy loss
def get_accuracy(self, Y_hat, Y):
"""
Compute the classification accuracy.
Args:
Y_hat (numpy.ndarray): Predicted probability matrix from the network, shape (n_classes, m).
Y (numpy.ndarray): One-hot encoded true labels, shape (n_classes, m).
Returns:
float: Accuracy as a fraction between 0 and 1.
"""
# TODO: Calculate the accuracy of the network
def test_on_letter(self, dataset):
kidnapping_letter = "v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs phfuvat bgurejvfr v nz va erny gebhoyr"
x = dataset.encode(kidnapping_letter).unsqueeze(0).to(self.device) # (1, T)
preds = self.forward(x)
preds = preds.argmax(dim=-1) # (1, T)
predicted_deciphered = "".join(dataset.idx2char[int(i)] for i in preds.squeeze(0))
print(f"\tInput (ROT13): {kidnapping_letter}")
print(f"\tPredicted original: {predicted_deciphered}")
return predicted_deciphered
def train(self, train_loader, epochs=100, learning_rate=0.001, verbose=True):
"""
Train the neural network using mini-batch gradient descent.
Args:
X (numpy.ndarray): Input data with shape (784, m), where each column is a flattened MNIST style image.
Y (numpy.ndarray): One-hot encoded labels with shape (n_classes, m), where n_classes is 26
epochs (int): Number of epochs for training.
learning_rate (float): Learning rate for the parameter updates.
batch_size (int, optional): Number of examples per mini-batch. Default is 32.
verbose (bool, optional): If True, prints training progress every 500 epochs. Default is False.
Returns:
dict: A dictionary containing:
- 'loss_history': List of loss values for each epoch.
- 'accuracy_history': List of accuracy values for each epoch.
Process:
- Shuffles the dataset each epoch.
- Processes data in mini-batches.
- Performs a forward pass, backpropagation, and parameter updates for each mini-batch.
- Computes the loss and accuracy for the entire dataset after each epoch.
"""
loss_history = []
accuracy_history = []
for i in range(epochs):
batch_losses = []
batch_accuracies = []
for X_batch, Y_batch in train_loader:
# Forward propagation
# TODO: Calculate the output of the network
# Calculate metrics for the whole epoch
loss = self.cross_entropy(Y_hat_batch, Y_batch)
accuracy = self.get_accuracy(Y_hat_batch, Y_batch)
batch_losses.append(loss.item())
batch_accuracies.append(accuracy.item())
# Backward propagation
# TODO: Calculate the gradients of the loss with respect to the input
# Update parameters
# TODO: Update the weights and biases of the layer using the learning rate
loss_history.append(np.mean(batch_losses))
accuracy_history.append(np.mean(batch_accuracies))
if verbose and i % (epochs // 4) == 0:
print(f"Epoch {i+1}/{epochs}")
print(f"loss: {loss_history[-1]:.5f}")
print(f"accuracy: {accuracy_history[-1]:.5f}")
print('Output test:')
self.test_on_letter(train_loader.dataset)
print("-" * 30)
return {'loss_history': loss_history, 'accuracy_history': accuracy_history}
vocab_size = dataset.vocab_size
padding_idx = dataset.padding_idx
# TODO: Instantiate the model, train it, and test it
Task 03-4: Reference Output (0 pts.)¶
Approximate Runtime: 6m 9.2s
Epoch 1/100
loss: 12.05548
accuracy: 0.04005
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: b<UNK>zi<PAD>ua<UNK>a<UNK>zauzbel<UNK>az<UNK>beuboue zioa<UNK>hb<UNK>beu<UNK>uobhbu<UNK>beu<UNK>lho<UNK><UNK>ho<UNK>beu<UNK>suz u<UNK>b<UNK>a<UNK>zauz<UNK><UNK>uhsie<UNK>ba<UNK>o<UNK>zu<UNK>bzz<UNK>lub<UNK>h<UNK>ho<UNK><UNK>bbe<UNK>bb<UNK>ho<UNK><UNK>uzz<UNK>eisu <UNK>zzo<UNK>eiziao<UNK> bl<UNK>zuo<UNK>i<UNK>b<UNK>beu<UNK><UNK>iazbehbbie<UNK>i <UNK>beu<UNK>shazi<UNK>g<UNK>hz<UNK>au<UNK>ie<UNK>zi<UNK>guz<UNK>ie<UNK>beu<UNK>ou<UNK>iea<UNK> ziiz<UNK>i <UNK> bb<SOS><UNK>ibeuz<UNK>bou<UNK>b<UNK>ha<UNK>be<UNK>zuhz<UNK>bzi<UNK>zzu
------------------------------
Epoch 26/100
loss: 0.57496
accuracy: 0.94361
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i lo<PAD>ed murderinz mr theisenaloyd at the estate the zas xas the peraect murder xeapon im sure ill zet axay xith it as xell hopeaully nobody aizures out the combination oa the padlocg abcde on locger on the second aloor oa ait<SOS> otherxise i am in real trouble
------------------------------
Epoch 51/100
loss: 0.20144
accuracy: 0.96861
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenyloyd at the estate the gas xas the peryect murder xeapon im sure ill get axay xith it as xell hopeyully nobody yigures out the combination oy the padlocg abcde on locger on the second yloor oy yit<SOS> otherxise i am in real trouble
------------------------------
Epoch 76/100
loss: 0.10249
accuracy: 0.98987
Output test:
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenfloyd at the estate the gas was the perfect murder weapon im sure ill get away with it as well hopefully nobody figures out the combination of the padlock abcde on locker on the second floor of fit<SOS> otherwise i am in real trouble
------------------------------
Input (ROT13): v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx nopqr ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Predicted original: i loved murdering mr theisenfloyd at the estate the gas was the perfect murder weapon im sure ill get away with it as well hopefully nobody figures out the combination of the padlock abcde on locker on the second floor of fit<SOS> otherwise i am in real trouble
Task 04: Transformer Comparisons¶
Similar to what we've been doing, lets see how our model stacks up against the actual pytorch implementat of a transformer!
Task 04-1: Description (0 pts.)¶
Positional Embedding Class¶
The first thing we'll need to do is create a special "positional-encoding" class so we can do all of that crazy sine wave stuff to modify our input vectors to reflect their location in the input text.
Task 04-1: Code (0 pts.)¶
import math
import torch
import torch.nn as nn
# --- PositionalEncoding unchanged ---
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len):
super().__init__()
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float()
* (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
self.register_buffer('pe', pe.unsqueeze(0)) # (1, max_len, d_model)
def forward(self, x): # x: (B, T, E)
return x + self.pe[:, :x.size(1)]
class Rot13TransformerEncoder(nn.Module):
"""
Encoder-only: forward(src) -> logits over vocab for each token (B, T, V).
Matches RNN behavior: aligned per-timestep prediction.
"""
def __init__(self, vocab_size, d_model, nhead, num_encoder_layers,
dim_feedforward, dropout, max_len, padding_idx):
super().__init__()
self.d_model = d_model
self.padding_idx = padding_idx
self.embedding = nn.Embedding(vocab_size, d_model, padding_idx=padding_idx)
self.pos_encoder = PositionalEncoding(d_model, max_len)
enc_layer = nn.TransformerEncoderLayer(
d_model=d_model, nhead=nhead,
dim_feedforward=dim_feedforward,
dropout=dropout, batch_first=True # <- no transposes
)
self.encoder = nn.TransformerEncoder(enc_layer, num_layers=num_encoder_layers)
self.fc_out = nn.Linear(d_model, vocab_size)
def forward(self, src): # src: (B, T) indices
key_padding_mask = (src == self.padding_idx) # (B, T) bool
kpm = key_padding_mask if key_padding_mask.any() else None
# TODO: Implement the forward pass
return logits
device = torch.device('cuda' if torch.cuda.is_available()
else "mps" if torch.backends.mps.is_available() else "cpu")
max_len = 512
model = Rot13TransformerEncoder(
vocab_size=dataset.vocab_size,
d_model=128,
nhead=4,
num_encoder_layers=2,
dim_feedforward=256,
dropout=0.1,
max_len=max_len,
padding_idx=dataset.padding_idx
).to(device)
# TODO: Instantiate the optimizer and loss function
def train(model, dataloader, optimizer, criterion, num_epochs):
model.train()
for epoch in range(num_epochs):
total = 0.0
for src, tgt_output in dataloader:
if tgt_output.dim() == 3:
tgt_output = tgt_output.argmax(dim=-1) # (B,T)
optimizer.zero_grad()
# TODO: Call the forward pass
B, T, V = logits.shape
loss = criterion(logits.reshape(B*T, V), tgt_output.reshape(B*T))
# TODO: Backpropagate and Gradient Descent
total += loss.item()
print(f"Epoch {epoch+1}, Loss: {total/len(dataloader):.4f}")
train(model, train_loader, optimizer, criterion, num_epochs=25)
kidnapping_letter = "v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx cynl ba ybpxre 69 ba gur frpbaq sybbe bs phfuvat bgurejvfr v nz va erny gebhoyr"
model.eval()
with torch.no_grad():
# Encode string to indices (1, T)
src = dataset.encode(kidnapping_letter).unsqueeze(0).to(device)
# Run through model
logits = model(src) # (1, T, V)
preds = logits.argmax(dim=-1) # (1, T)
# Decode predicted indices back to string
output_str = dataset.decode(preds.squeeze(0))
print(f"Input: {kidnapping_letter}")
print(f"Output: {output_str}")
Task 04-3: Reference Output (0 pts.)¶
Approximate Runtime: 3m 2.3s
Epoch 1, Loss: 0.1295
Epoch 2, Loss: 0.0029
Epoch 3, Loss: 0.0013
Epoch 4, Loss: 0.0008
Epoch 5, Loss: 0.0005
Epoch 6, Loss: 0.0004
Epoch 7, Loss: 0.0003
Epoch 8, Loss: 0.0002
Epoch 9, Loss: 0.0002
Epoch 10, Loss: 0.0001
Epoch 11, Loss: 0.0001
Epoch 12, Loss: 0.0001
Epoch 13, Loss: 0.0001
Epoch 14, Loss: 0.0001
Epoch 15, Loss: 0.0001
Epoch 16, Loss: 0.0000
Epoch 17, Loss: 0.0000
Epoch 18, Loss: 0.0000
Epoch 19, Loss: 0.0000
Epoch 20, Loss: 0.0000
Epoch 21, Loss: 0.0000
Epoch 22, Loss: 0.0000
Epoch 23, Loss: 0.0000
Epoch 24, Loss: 0.0000
Epoch 25, Loss: 0.0000
Input: v ybirq zheqrevat ze gurvfrasyblq ng gur rfgngr gur tnf jnf gur cresrpg zheqre jrncba vz fher vyy trg njnl jvgu vg nf jryy ubcrshyyl abobql svtherf bhg gur pbzovangvba bs gur cnqybpx 69 ba ybpxre ba gur frpbaq sybbe bs svgm bgurejvfr v nz va erny gebhoyr
Output: i loved murdering mr theisenfloyd at the estate the gas was the perfect murder weapon im sure ill get away with it as well hopefully nobody figures out the combination of the padlock ee on locker on the second floor of fitz otherwise i am in real trouble
Task 04-4: Transformer Short Answer Questions (2 pts.)¶
What are some benefits of transformers compared to RNNs?
- [ANSWER]
What do Q, K, and V stand for and what do they represent?
- [ANSWER]
Task 05: Final Evidence Collection¶
Task 05-1: Selfie with Evidence (1 pt.)¶
Actually photographing the evidence¶
Now that you have the code for the locker, hopefully you have enough to put this villain behind bars! Head over to the locker and open it, take a picture of the evidence and yourselves and submit it along with your code, the TAs will handle the police report! Remember, this is an active investigation and tampering with the evidence will result in a felony charge!
NOTE: You can just submit your photo as a file on github alongside your notebook. All group-members need to be in the photo for credit.